09/29/07

Although it is difficult to give an accurate date as to when the problem of trisecting an angle first appeared, we do know that Hippocrates, who made the first major contribution to the problems of squaring a circle and doubling a cube, also studied the problem of trisecting an angle. There is a fairly straightforward way to trisect any angle which was known to Hippocrates.

It works as follows. Given an angle CAB then draw CD perpendicular to AB to cut it at D. Complete the rectangle CDAF. Extend FC to E and let AE be drawn to cut CD at H. Have the point E chosen so that HE = 2AC. Now angle EAB is 1/3 of angle CAB.

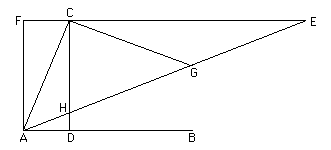
To see this let G be the midpoint of HE so that HG = GE = AC. Since ECH is a right angle, CG = HG = GE. Now angle EAB = angle CEA = angle ECG. Also since AC = CG we have angle CAG = angle CGA. But angle CGA = angle GEC + angle ECG = 2 CEG = 2 EAB as required.