09/29/07

Abu Ja'far Muhammad ibn Musa al-Khwarizmi:

The treatise Hisab al-jabr w'al-muqabala was the most famous and important of all of al-Khwarizmi's works. In this book, which has given us the word 'algebra', al-Khwarizmi gives a complete solution to all possible types of quadratic equation. His equations are linear or quadratic and are composed of units, roots and squares. For example, to al-Khwarizmi a unit was a number, a root was x, and a square was x². However, although we shall use the now familiar algebraic notation in this article to help the reader understand the notions, Al-Khwarizmi's mathematics is done entirely in words with no symbols being used.

He first reduces an equation (linear or quadratic) to one of six standard forms:
1. Squares equal to roots.
2. Squares equal to numbers.
3. Roots equal to numbers.
4. Squares and roots equal to numbers; e.g. x² + 10 x = 39.
5. Squares and numbers equal to roots; e.g. x² + 21 = 10 x.
6. Roots and numbers equal to squares; e.g. 3 x + 4 = x².

The reduction is carried out using the two operations of al-jabr and al-muqabala. Here "al-jabr" means "completion" and is the process of removing negative terms from an equation. For example, using one of al-Khwarizmi's own examples, "al-jabr" transforms x² = 40 x - 4 x² into 5 x² = 40 x. The term "al-muqabala" means "balancing" and is the process of reducing positive terms of the same power when they occur on both sides of an equation. For example, two applications of "al-muqabala" reduces 50 + 3 x + x² = 29 + 10 x to 21 + x² = 7 x (one application to deal with the numbers and a second to deal with the roots).

Al-Khwarizmi then shows how to solve the six standard types of equations. He uses both algebraic methods of solution and geometric methods. For example to solve the equation x² + 10 x = 39 he writes :-
... a square and 10 roots are equal to 39 units. The question therefore in this type of equation is about as follows: what is the square which combined with ten of its roots will give a sum total of 39? The manner of solving this type of equation is to take one-half of the roots just mentioned. Now the roots in the problem before us are 10. Therefore take 5, which multiplied by itself gives 25, an amount which you add to 39 giving 64. Having taken then the square root of this which is 8, subtract from it half the roots, 5 leaving 3. The number three therefore represents one root of this square, which itself, of course is 9. Nine therefore gives the square.

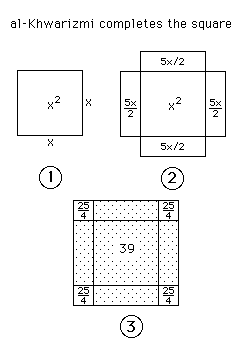The geometric proof by completing the square follows. Al-Khwarizmi starts with a square of side x, which therefore represents x² (Figure 1). To the square we must add 10x and this is done by adding four rectangles each of breadth 10/4 and length x to the square (Figure 2). Figure 2 has area x² + 10 x which is equal to 39. We now complete the square by adding the four little squares each of area 5/2 5/2 = 25/4. Hence the outside square in Fig 3 has area 4 25/4 + 39 = 25 + 39 = 64. The side of the square is therefore 8. But the side is of length 5/2 + x + 5/2 so x + 5 = 8, giving x = 3.
 

Here is al-Khwarizmi's solution of the equation
x² + 21 = 10x.
What is most remarkable is that in this case he knows that the quadratic has two solutions:-

Halve the number of the roots. It is 5. Multiply this by itself and the product is 25. Subtract from this the 21 added to the square term and the remainder is 4. Extract its square root, 2, and subtract this from half the number of roots, 5. There remains 3. This is the root you wanted, whose square is 9. Alternatively, you may add the square root to half the number of roots and the sum is 7. This is then the root you wanted and the square is 49.

Now it is clear that al-Khwarizmi is intending to teach his readers general methods of solution and not just how to solve specific examples. This is clear from the was that he continues:-

When you meet an instance which refers you to this case, try its solution by addition, and if that does not work subtraction will. In this case, both addition and subtraction can be used, which will not serve in any other of the three cases where the number of roots is to be halved.
Know also that when, in a problem leading to this case, you have multiplied half the number of roots by itself, if the product is less than the number of dirhams added to the square term, then the case is impossible. On the other hand, if the product is equal to the dirhams themselves, then the root is half the number of roots