مسوّدہ بخشالی
The Bakhshali manuscript is an early mathematical manuscript which was
discovered over 100 years ago. We shall discuss in a moment the problem of
dating this manuscript, a topic which has aroused much controversy, but for
the moment we will examine how it was discovered. The paper describes this
discovery along with the early history of the manuscript. Gupta writes:-
The Bakhshali Manuscript is the name given to the mathematical work written
on birch bark and found in the summer of 1881 near the village Bakhshali (or
Bakhshalai) of the Yusufzai subdivision of the Peshawar district (now in
Pakistan). The village is in Mardan tahsil and is situated 50 miles from the
city of Peshawar.
An Inspector of Police named Mian An-Wan-Udin (whose tenant actually
discovered the manuscript while digging a stone enclosure in a ruined place)
took the work to the Assistant Commissioner at Mardan who intended to
forward the manuscript to Lahore Museum. However, it was subsequently sent
to the Lieutenant Governor of Punjab who, on the advice of General A
Cunningham, directed it to be passed on to Dr Rudolf Hoernle of the Calcutta
Madrasa for study and publication. Dr Hoernle presented a description of the
BM before the Asiatic Society of Bengal in 1882, and this was published in
the Indian Antiquary in 1883. He gave a fuller account at the Seventh
Oriental Conference held at Vienna in 1886 and this was published in its
Proceedings. A revised version of this paper appeared in the Indian
Antiquary of 1888. In 1902, he presented the Bakhshali Manuscript to the
Bodleian Library, Oxford, where it is still (Shelf mark: MS. Sansk. d. 14).
A large part of the manuscript had been destroyed and only about 70 leaves
of birch-bark, of which a few were only scraps, survived to the time of its
discovery.
To show the arguments regarding its age we note that F R Hoernle, referred
to in the quotation above, placed the Bakhshali manuscript between the third
and fourth centuries AD. Many other historians of mathematics such as Moritz
Cantor, F Cajori, B Datta, S N Sen, A K Bag, and R C Gupta agreed with this
dating. In 1927-1933 the Bakhshali manuscript was edited by G R Kaye and
published with a comprehensive introduction, an English translation, and a
transliteration together with facsimiles of the text. Kaye claimed that the
manuscript dated from the twelfth century AD and he even doubted that it was
of Indian origin.
Channabasappa gives the range 200 - 400 AD as the most probable date. In the
same author identifies five specific mathematical terms which do not occur
in the works of Aryabhata and he argues that this strongly supports a date
for the Bakhshali manuscript earlier than the 5th century. Joseph
suggests that the evidence all points to the:-
... manuscript [being] probably a later copy of a document composed at some
time in the first few centuries of the Christian era.
L V Gurjar claims that the manuscript is no later than 300 AD. On the
other hand T Hayashi claims that the date of the original is probably
from the seventh century, but he also claims that the manuscript itself is a
later copy which was made between the eighth and the twelfth centuries AD.
I [EFR] feel that if one weighs all the evidence of these experts the most
likely conclusion is that the manuscript is a later copy of a work first
composed around 400 AD. Why do I believe that the actual manuscript was
written later? Well our current understanding of Indian numerals and writing
would date the numerals used in the manuscript as not having appeared before
the ninth or tenth century. To accept that this style of numeral existed in
400 AD. would force us to change greatly our whole concept of the time-scale
for the development of Indian numerals. Sometimes, of course, we are forced
into major rethinks but, without supporting evidence, everything points to
the manuscript being a tenth century copy of an original from around 400 AD.
Despite the claims of Kaye, it is essentially certain that the manuscript is
Indian.
The attraction of the date of 400 AD for the Bakhshali manuscript is that
this puts it just before the "classical period" of Indian mathematics which
began with the work of Aryabhata I around 500. It would then fill in
knowledge we have of Indian mathematics for, prior to the discovery of this
manuscript, we had little knowledge of Indian mathematics between the dates
of about 200 BC. and 500 AD. This date would make it a document near the end
of the period of Jaina mathematics and it can be seen as, in some sense,
marking the achievements of the Jains.
What does the manuscript contain? Joseph writes :-
The Bakhshali manuscript is a handbook of rules and illustrative examples
together with their solutions. It is devoted mainly to arithmetic and
algebra, with just a few problems on geometry and mensuration. Only parts of
it have been restored, so we cannot be certain about the balance between
different topics.
Now the way that the manuscript is laid out is quite unusual for an Indian
document (which of course leads people like Kaye to prefer the hypothesis
that it is not Indian at all - an idea in which we cannot see any merit).
The Bakhshali manuscript gives the statement of a rule. There then follows
an example given first in words, then using mathematical notation. The
solution to the example is then given and finally a proof is set out.
The notation used is not unlike that used by Aryabhata but it does have
features not found in any other document. Fractions are not dissimilar in
notation to that used today, written with one number below the other. No
line appears between the numbers as we would write today, however. Another
unusual feature is the sign + placed after a number to indicate a negative.
It is very strange for us today to see our addition symbol being used for
subtraction. As an example, here is how 3/4 - 1/2 would be written.

Compound fractions were written in three lines. Hence 1 plus
1/3 would be written thus

and 1 minus 1/3 =
2/3 in the following way
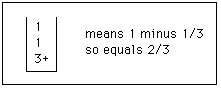
Sums of fractions such as 5/1 plus
2/1 are written using the symbol yu ( for yuta)

Division is denoted by bha, an abbreviation for bhaga meaning
"part". For example
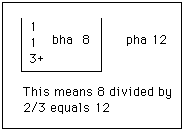
Equations are given with a large dot representing the unknown.
A confusing aspect of Indian mathematics is that this notation was also often
used to denote zero, and sometimes this same notation for both zero and the
unknown are used in the same document. Here is an example of an equation as it
appears in the Bakhshali manuscript.

The method of equalization is found in many types of problems which occur in
the manuscript. Problems of this type which are found in the manuscript are
examined and some of these lead to indeterminate equations. Included
are problems concerning equalizing wealth, the positions of two travelers,
wages, and purchases by a number of merchants. These problems can all be
reduced to solving a linear equation with one unknown or to a system of n
linear equations in n unknowns. To illustrate we give the following
indeterminate problem which, of course, does not have a unique solution:-
One person possesses seven asava horses, another nine haya horses, and
another ten camels. Each gives two animals, one to each of the others. They
are then equally well off. Find the price of each animal and the total value
of the animals possesses by each person.
The solution, translated into modern notation, proceeds as follows. We seek
integer solutions x1, x2,
x3 and k (where x1 is the price
of an asava, x2 is the price of
a haya, and x3 is the price of a
horse) satisfying
5 x1 + x2
+ x3 = x1 + 7
x2+ x3
= x1 + x2 + 8x3 = k.
Then 4 x1 = 6 x2 = 7 x3 = k - (x1
+ x2 + x3).
For integer solutions k - (x1 +
x2 + x3)
must be a multiple of the lcm of 4, 6 and 7. This is the indeterminate
nature of the problem and taking different multiples of the lcm will lead to
different solutions. The Bakhshali manuscript takes k - (x1
+ x2 + x3)
= 168 (this is 4 6 7) giving x1 = 42, x2 = 28, x3 = 24. Then k = 262 is the
total value of the animals possesses by each person. This is not the minimum
integer solution which would be k = 131.
If we use modern methods we would solve the system of three equation for x1,
x2, x3
in terms of k to obtain
x1 = 21k/131, x2
= 14k/131, x3 = 12k/131
so we obtain integer solutions by taking k = 131 which is the smallest
solution. This solution is not given in the Bakhshali manuscript but the
author of the manuscript would have obtained this had he taken k - (x1
+ x2 + x3)
= lcm(4, 6, 7) = 84.
Here is another equalization problem taken from the manuscript which has a
unique solution:-
Two page-boys are attendants of a king. For their services one gets 13/6
dinaras a day and the other 3/2. The first owes the second 10 dinaras.
calculate and tell me when they have equal amounts.
Now I would solve this by saying that the first gets 13/6 - 3/2 = 2/3
dinaras more than the second each day. He needs 20 dinaras more than the
second to be able to give back his 10 dinaras debt and have them with equal
amounts. So 30 days are required when each has 13 30/6 - 10 = 55 dinaras.
This is not the method of the Bakhshali manuscript which uses the "rule of
three".
The rule of three is the familiar way of solving problems of the type: if a
man earns 50 dinaras in 8 days how much will he earn in 12 days. The
Bakhshali manuscript describes the rule where the three numbers are written
8 50 12
The 8 is the "pramana", the 50 is the "phala" and the 12 is the "iccha". The
rule, according to the Bakhshali manuscript gives the answer as
phala iccha/pramana
or in the case of the example 50 12/8 = 75 dinaras.
Applying this to the page-boy problem we obtain equal amounts for the
page-boys after n days where
13 n/6 = 3 n/2 +20
so n = 30 and each has 13 30/6 - 10 = 55 dinaras.
Another interesting piece of mathematics in the manuscript concerns
calculating square roots. The following formula is used
√Q = √(A2 + b) = A + b/2A -
(b/2A)2/(2(A + b/2A))
This is stated in the manuscript as follows:-
In the case of a non-square number, subtract the nearest square number,
divide the remainder by twice this nearest square; half the square of this
is divided by the sum of the approximate root and the fraction. this is
subtracted and will give the corrected root.
Taking Q = 41, then A = 6, b = 5 and we obtain 6.403138528 as the
approximation to √41 = 6.403124237. Hence we see that the Bakhshali formula
gives the result correct to four decimal places.
The Bakhshali manuscript also uses the formula to compute √105 giving
10.24695122 as the approximation to √105 = 10.24695077. This time the
Bakhshali formula gives the result correct to five decimal places.
The following examples also occur in the Bakhshali manuscript where the
author applies the formula to obtain approximate square roots:
√487
Bakhshali formula gives 22.068076490965
Correct answer is 22.068076490713
Here 9 decimal places are correct
√889
Bakhshali formula gives 29.816105242176
Correct answer is 29.8161030317511
Here 5 decimal places are correct
[Note. If we took 889 = 302 - 11 instead of 292 + 48 we would get
Bakhshali formula gives 29.816103037078
Correct answer is 29.8161030317511
Here 8 decimal places are correct]
√339009
Bakhshali formula gives 582.2447938796899
Correct answer is 582.2447938796876
Here 11 decimal places are correct
It is interesting to note that Channabasappa derives from the
Bakhshali square root formula an iterative scheme for approximating square
roots. He finds that it is 38% faster than Newton's method in giving
√41 to ten places of decimals.

