










|
|
عمر خیّام The Moving Finger writes, and,
having writ,
Moves on: nor all thy Piety nor Wit
Shall lure it back to cancel half a Line,
Nor all thy Tears wash out a Word of it.
Omar Khayyam wrote several works including Problems of Arithmetic, a book on
music and one on algebra before he was 25 years old.
Khayyam measured the length of the year as 365.24219858156 days. Two
comments on this result. Firstly it shows an incredible confidence to
attempt to give the result to this degree of accuracy. We know now that the
length of the year is changing in the sixth decimal place over a person's
lifetime. Secondly it is outstandingly accurate. For comparison the length
of the year at the end of the 19th century was 365.242196 days, while today
it is 365.242190 days.
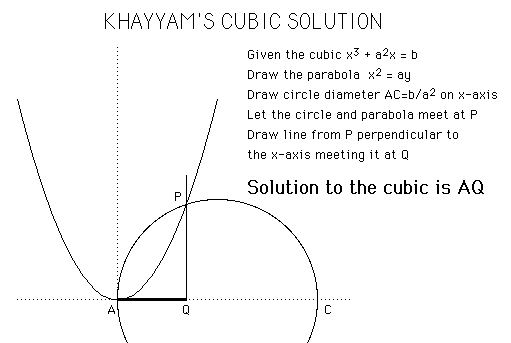
His Treatise on Demonstration of Problems of Algebra which contained a
complete classification of cubic equations with geometric solutions found by
means of intersecting conic sections.
|

